Univariate Statistik
Unter dem Begriff „univariate Statistik“ versteht man die isolierte Betrachtung einzelner Merkmale bzw. Variablen von Untersuchungseinheiten (= Personen). Man macht nur Aussagen über ein einziges Merkmal (z.B. Alter). Bedeutsame Informationen liefern dabei Lagemaße und Streumaße.
Beispiel für eine Verteilung
Im Folgenden finden Sie ein Beispiel für eine eindimensionale Verteilung.
Erhoben wurde hierbei das Merkmal Alter.
Die ursprüngliche Zuordnung einer Merkmalsausprägung zu einer Person nennt man Urliste:
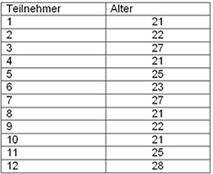
Ordnet man die Urliste nach Stärke der Merkmalsausprägung ergibt sich die sortierte Liste daraus:
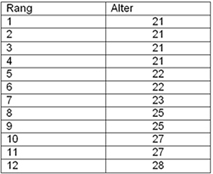
Diese kann man zur Häufigkeitsverteilung zusammenfassen:
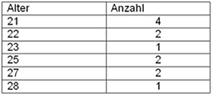
Es gilt: Die Summe der Häufigkeiten (Anzahl) ergibt die Gesamtanzahl der Teilnehmer N = (4+2+1+2+2+1) = 12





