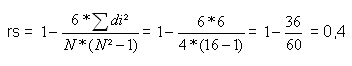Rangkorrelationskoeffizient Spearmans rho
Dieses Maß ist ab ordinalem Skalenniveau gültig und betrachtet die Rangplatzdifferenz (di) von zwei verschiedenen Beurteilungen bei zwei ordinalskalierten Merkmalen
Beispiel:
Die Teilnehmerinnen an einem Eiskunstlauf-Wettbewerb werden von zwei Punktrichtern (Punktrichter A und Punktrichter B) bewertet. Nun stellt sich die Frage, ob die Läuferinnen die von Punktrichter A gut bewertet wurden (x-Wert) tendenziell auch von Punktrichter B gut bewertet wurden (y-Wert).
Es werden nun zunächst alle x-Werte und alle y-Werte in Ränge umgewandelt. Demzufolge besitzt jede Läuferin einen Rang x und einen Rang y. Die Differenz Rang x – Rang y ergibt dann die Rangdifferenz di, welche später aufaddiert in die Formel eingesetzt wird.
Für die Berechnung von Spearman?s rho mit der mathematischen Formel ist es notwendig, nicht die ordinalen Ausgangswerte, sondern die Ränge zu verwenden. Diese werden dann quasi wie echte metrische Zahlen behandelt.
Die Formel für Spearmans rho lautet:
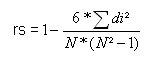
Ein Beispiel zur Verdeutlichung: Aufgelistet finden Sie die Noten von zwei Punktrichtern beim Eiskunstlauf für 4 Läuferinnen.

Zuerst werden aus den Noten von Punktrichter A Ränge gebildet. Diejenige Läuferin, die die beste Note bekommen hat erhält Rang 1, die mit der zweitbesten Note Rang zwei usw. Analog werden anschließend die Ränge für Punktrichter B gebildet.
Spezialfall: Wenn zwei Läuferinnen von einem Punktrichter dieselbe Note erhalten, wird der Durchschnittsrang berechnet (z.B. beide Läuferinnen erhalten die Bestnote 5,6 zu vergeben wären die Ränge 1 und 2 beide erhalten dann Rang (1+2)/2 = 1,5).
Wichtig: Die Formel für Spearman?s rho ist nur gültig, wenn weniger als 20% der vergebenen Ränge dem oben beschriebenen Spezialfall entsprechen, d.h. weniger als 20% der vergebenen Ränge sind gleich.
Für das obige Beispiel entsteht folgende Rangtabelle:

Nun werden die Rangdifferenzen (A-B) berechnet:

Die Summe aus di² beträgt 6. N beträgt 4 (da hier 4 Läuferinnen bewertet wurden).
Die Berechnung von rs ergibt folgendes: